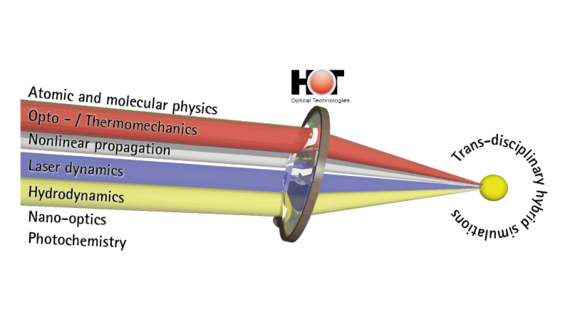
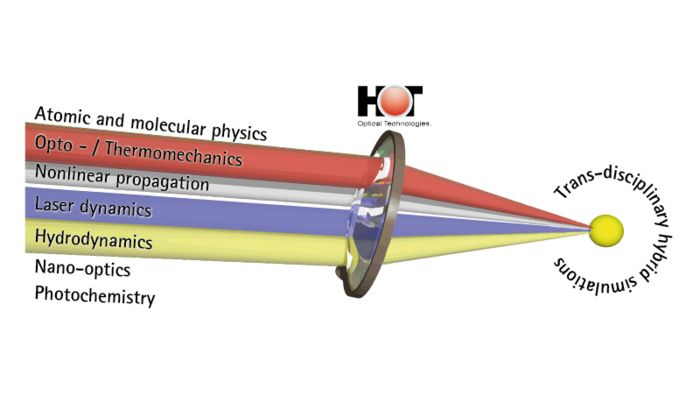
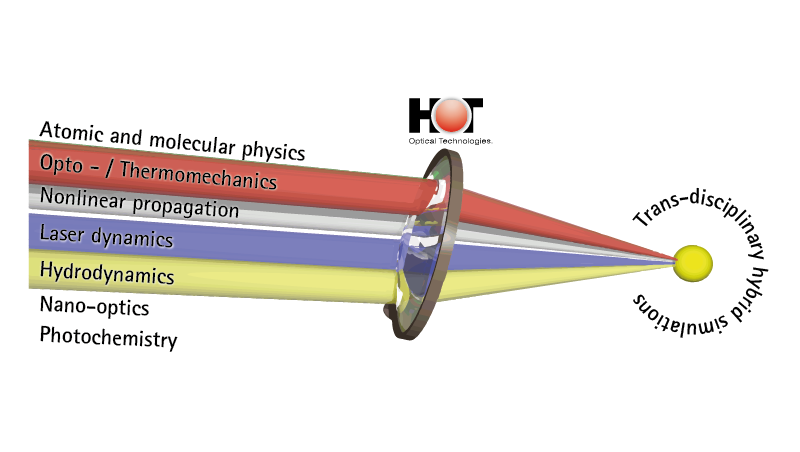
Wir entwickeln neuartige hybride und multiskalige numerische Konzepte zur umfassenden Beschreibung und Modellierung von Lichtfeldern in optischen Medien. Unsere Ansätze profitieren maßgeblich von modernen Trends in der Computertechnologie und insbesondere von der massiven Parallelisierung mit Grafikkarten (GPUs). Diese ermöglichen letztlich eine effiziente Simulation bei relativ moderaten Kosten und gleichzeitig großer Rechenleistung, die bisher nur mit Computerclustern erreicht werden konnte. Die in unserer Forschung entwickelten Simulationstools umfassen mehrere Größenordnungen von Atomen und Molekülen bis hin zu Nanopartikeln und Bulk-Strukturen. Die Materialklassen reichen von Dielektrika über Halbleiter, Flüssigkeiten und biologischem Gewebe bis hin zu funktionellen / aktiven Verbundmaterialien. Unser umfassender Ansatz zielt darauf ab, alle relevanten Aspekte der Licht-Materie-Interaktion zu modellieren und zu simulieren, z.B. optische sowie thermische, mechanische oder akustische Effekte auf allen relevanten Längen- und Zeitskalen. Dies ermöglicht es uns, etwa die Materialantwort, also thermische Effekte, in der Beschreibung der Lichtausbreitung zu beschreiben.
Projekte
- Projekt 1: Simulation of light tissue interaction
- Projekt 2: Thermo-mechanical simulation of integrated polymer photonic devices
- Projekt 3: Dynamic light propagation in high performance fibre amplifier
- Projekt 4: Generation of supercontinuum in silicon waveguides
- Projekt 5: Simulation of the opto mechanic behavior of laser based illumination systems
- Projekt 6: Structural and optical properties of dielectric layers
- Projekt 7: Simulation of the light-guiding properties in coaxially flowing fluid pairs using wave optical light propagation in fluid-dynamically and thermally superimposed refractive index distributions
Sprecher

 © PhoenixD
© PhoenixD
30167 Hannover

 © PhoenixD
© PhoenixD
Leiter von Hymnos


30167 Hannover


